What is (A*) A-Star Algorithm? Empowered: With 3 Advantages and Disadvantages

Introduction to A* or A-Star Algorithm

The A* (pronounced “A-star”) algorithm is a highly versatile and widely used graph traversal and pathfinding algorithm. It’s a popular choice in various applications, including game development, robotics, and navigation systems, due to its ability to intelligently find optimal paths within complex environments. In this article, we’ll delve into the workings of the A* algorithm, its core concepts, advantages, disadvantages, and why it’s indispensable in many domains.

What is A* Algorithm?

The A* algorithm is a popular pathfinding algorithm used in computer science and artificial intelligence. It’s often employed to find the shortest path from a starting point to a goal node in a graph or a grid-like environment.

What Is the A-Star Algorithm?

At its core, A* is a best-first search algorithm. It aims to find the least-cost path from a given starting node to a goal node in a weighted graph. The weights on the graph’s edges can represent distances, travel times, costs, or other factors relevant to the problem domain.

Core Concept of the A-Star Algorithm (A*)

The key to A*’s efficiency lies in its evaluation function:

f(n) = g(n) + h(n)

where:

• n: The current node being evaluated
• f(n): The estimated total cost of the cheapest solution path from the start to the goal, passing through node ‘n’.
• g(n): The actual cost to reach node ‘n’ from the start node.
• h(n): A heuristic estimate of the cost from node ‘n’ to the goal node.

How Does A-Star Algorithm Work?

1. Initialization: The algorithm starts with an ‘open list’ containing only the start node.
2. Node Selection: At each iteration, the node with the lowest f(n) value is removed from the open list. If it’s the goal node, the algorithm terminates with success.
3. Expansion: For each neighbor of the selected node:
   • Calculate g(neighbor) – the cost to reach the neighbor from the start.
   • If the neighbor is not in the open list or has a lower g(neighbor) value than before, update its values:
     • Set its parent to the currently selected node.
     • Calculate and store g(neighbor).
     • Calculate h(neighbor).
     • Add the neighbor to the open list.
4. Closed List: The selected node is added to a ‘closed list’ to prevent it from being revisited.
5. Repeat: The algorithm continues from step 2 until the goal is reached or the open list is empty (no solution exists).

Heuristics in A-Star Algorithm

The choice of heuristic function (h(n)) is crucial for the performance of A*:

• Admissible Heuristics: An admissible heuristic never overestimates the cost of reaching the goal. Examples include:
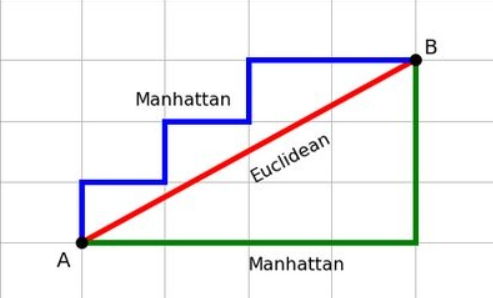
  • Manhattan Distance: The sum of absolute differences in X and Y coordinates (good for grid-based maps).
  • Euclidean Distance: Straight-line distance (great if no obstacles are present).

• Inadmissible Heuristics: These heuristics might overestimate the cost to the goal. They can sometimes lead to faster path discovery, but optimality is no longer guaranteed.
• Consistent Heuristics: A stronger version of admissibility. Consistent heuristics ensure that the h value for a node is always less than or equal to the cost of moving to a neighbor plus the h value of that neighbor.

Advantages of A-star Algorithm

• Optimality: If the chosen heuristic is admissible, A* is guaranteed to find the shortest path to the goal (provided a solution exists).
• Efficiency: A* often outperforms uninformed search algorithms due to its directed exploration guided by the heuristic function.
• Flexibility: A* is adaptable to various problem domains by modifying the cost function and heuristic, making it suitable for a wide range of applications.

Disadvantages of A-Star Algorithm

• Memory-Intensive: A* can consume substantial memory, particularly for large or complex search spaces. Keeping track of open and closed lists incurs a memory cost.
• Heuristic Sensitivity: The performance of A* heavily depends on the quality of the heuristic function. If the heuristic is too inaccurate, it might misguide the search and lead to longer exploration times.
• Completeness on Infinite Graphs: A* is complete (guaranteed to find a solution if one exists) on finite graphs with non-negative edge weights. However, its completeness is not guaranteed on infinite graphs.

Conclusion

The A* algorithm is a powerful and versatile tool for solving pathfinding problems in a variety of domains. Its core strength lies in the balance between exploiting existing knowledge (g(n)) and making informed estimations about future costs (h(n)). When equipped with an admissible heuristic, A* provides optimal solutions efficiently.

Despite potential memory constraints and sensitivity to the choice of heuristic, A* remains an invaluable algorithm in the field of computer science and has played a significant role in advancements within game AI, navigation systems, and many other exciting applications.