Constraint Satisfaction Problem – Essential Components, 1 Example and Various Solution Methods.

Constraint Satisfaction Problem:

A constraint satisfaction problem (CSP) is a type of problem where you need to find settings for different elements, following certain rules. It’s like a puzzle with specific restrictions on how the pieces can fit together. Here’s a breakdown to understand it better. CSPs are a fundamental concept in computer science and artificial intelligence, providing a powerful framework for modeling and solving various real-world problems.

Components of Constraint Satisfaction Problem:

1. Variables: These are the elements you need to assign values to. Imagine them as the blank spaces in a crossword puzzle.
   X = { X₁ , X₂ , . . . , X_n }, where X_i denotes an individual variable.
2. Domains: A domain is the set of possible values that a variable can take. Like the letters you can use to fill in the crossword blanks.
   D = { D₁ , D₂ , . . . , D_n }, where D_i represents the domain of variable 𝑋𝑖​.
3. Constraints: Constraints specify the rules that the variables must satisfy. These rules limit how you can assign values to the variables. These are They define which combinations of values are valid for the problem. They act like the rules in a game, ensuring everything fits together correctly.
   C = {C₁ , C₂ , . . . , C_m }, where C_j defines a constraint over a subset of variables.

Example: Sudoku Puzzle

Sudoku is a classic puzzle that can be represented as a constraint satisfaction problem. In Sudoku, we aim to fill a 9×9 grid with digits from 1 to 9, such that each row, each column, and each 3×3 subgrid contains all the digits from 1 to 9 without repetition.

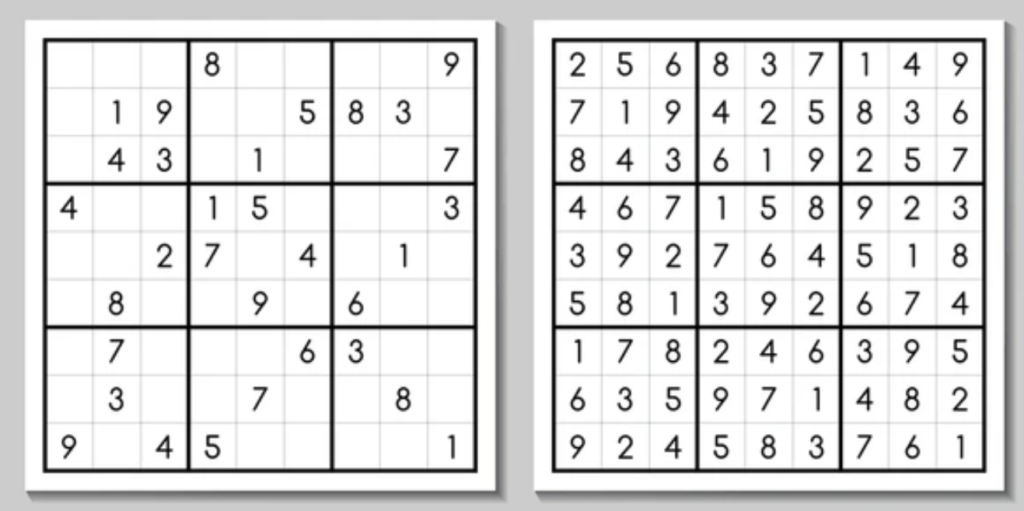
Formal Representation:

• Variables: The empty cells in the Sudoku grid.
  X={ X_i,j |  1 ≤ i,j ≤ 9 } , where X_i,j represents the cell in the 𝑖th row and 𝑗th column
• Domains: The numbers 1 to 9, representing the possible values that can be placed in that cell.
  D_i,j = { 1 , 2 , . . . , 9 }
• Constraints:
  1. Each row must contain all digits 1 to 9 exactly once.
     C_row = { X_i,1 ≠ X_i,2 , X_i,1 ≠ X_i,3 , . . . , X_i,8 ≠ X_i,9 }
  2. Each column must contain all digits 1 to 9 exactly once.
     C_col = { X_1,j ≠ X_2,j , X_1,j ≠ X_3,j , . . . , X_8,j ≠ X_9,j }
  3. Each 3×3 sub-grid must contain all digits 1 to 9 exactly once.
     C_subgrid = { X_1,1 ≠ X_1,2 , X_1,1 ≠ X_1,3 , . . . , X_3,3 ≠ X_3,2, X_3,3 ≠ X_2,3 }

This formal representation enables us to apply CSP solving techniques to solve Sudoku puzzles efficiently. We can use backtracking search algorithms with constraint propagation to find valid solutions satisfying all constraints.

Solving Constraint Satisfaction Problems

There are various algorithms and techniques have been developed to tackle CSPs efficiently, some of these are:

• 1. Constraint Propagation:
  Constraint propagation means using the rules of the problem to limit our choices.
  How it works: It checks if the values we pick for one thing affect what we can pick for something else. If they do, it updates our options based on those rules.
  • Arc Consistency: Makes sure that the values we pick for one variable won’t cause problems with the values in another variable that it’s connected to.
  • Domain Reduction: Gets rid of values from variables that don’t fit with the rules.
  • Propagation Techniques: Like checking values as we go to see if they still make sense with the rules.
    
• 2. Backtracking Search Algorithm
  Backtracking is like trying out different options, and if we hit a dead end, we go back and try something else.
  How it works: We make a guess, and if it doesn’t work, we backtrack and try another guess. It’s like exploring a maze by going down one path and backing up if it’s a dead end.
  • Recursive Search: We keep going deeper into the problem, trying out different combinations of values until we find a solution.
  • Depth-First Search: We focus on trying out one path at a time, going deep into the problem before trying a different path.
    
• 3. Forward Checking
  Forward checking helps us eliminate some choices early on.
  How it works: After we make a choice, forward checking looks ahead to see if that choice blocks any other options. If it does, it crosses those options off.
  Basic Principle: We don’t waste time exploring paths that we know won’t lead to a solution.
  
• 4. Backjumping
  Backjumping helps us skip over some wrong turns.
  How it works: Instead of just going back one step when we hit a dead end, backjumping lets us go back further, skipping over some bad choices we made earlier.
  Basic Principle: It’s like learning from our mistakes and going back to the point where things went wrong, instead of starting all over again.
  
• 5. Conflict-Directed Backjumping (CBJ)
  CBJ is like backjumping with a better map.
  How it works: When we hit a dead end, CBJ helps us figure out exactly where we went wrong and how far back we need to go to fix it.
  Basic Principle: It’s like finding the specific problem and going back directly to solve it, instead of guessing where the issue might be.
  
• 6. Heuristics for Variable and Value Ordering
  They’re like smart strategies for picking what to try next.
  Variable Ordering: It’s about picking which thing to decide on first.
  Value Ordering: It’s about picking which option to try first for that thing.

Advanced Topics in CSPs

• Local Search Algorithms for CSPs
  • Overview: These algorithms iteratively improve solutions by making small changes.
  • Basic Idea: Start with a solution and tweak it until it’s good enough.
  • Examples: Hill climbing, simulated annealing.
  • Applications: Useful for large problems where finding the best solution is tough.

• Constraint Handling Rules (CHR)
  • Definition: CHR is a language for writing constraint solvers.
  • Basic Idea: Provides rules for defining and simplifying constraints.
  • Features: Helps specify complex constraints and automate simplification.
  • Applications: Used in constraint programming and AI.

• Constraint Optimization Problems (COPs)
  • Definition: COPs add optimization to CSPs.
  • Basic Idea: Besides satisfying rules, aim to optimize a criteria.
  • Techniques: Use local search, mathematical programming, etc.
  • Applications: Common in scheduling, planning, and decision-making.

• Hybrid Approaches and Applications
  • Definition: Combine different methods for better results.
  • Basic Idea: Mix and match techniques to solve tough problems.
  • Examples: Combine local search with constraint propagation.
  • Applications: Used in robotics, bioinformatics, etc., for complex problem-solving.

Importance and Applications in Various Fields:

CSPs find applications in numerous domains including:

• Artificial Intelligence: CSPs are extensively used in AI for tasks such as planning, scheduling, and resource allocation.
• Robotics: Robot motion planning and task scheduling can be formulated as CSPs.
• Bioinformatics: Problems in genetics, protein folding, and molecular structure prediction can be solved using CSP techniques.
• Operations Research: CSPs are applied in logistics, supply chain management, and optimization problems.
• Computer Vision: Image processing tasks like object recognition and image segmentation can be formulated as CSPs.